Como ya lo notaron Brian Miller y Cornelius Hunter, Winston Ewert acaba de publicar un artículo científico extraordinario. Escribiendo en la revista BIO-Complexity, Ewert propone que la vida se explica mejor no por la hipótesis de Darwin de un árbol de antepasado común, sino por una hipótesis moderna inspirada en el diseño de un gráfico de dependencia. El modelo de gráfico de dependencia se ha explicado aquí. El documento original está aquí.
Quiero explicar las matemáticas y la filosofía que nos permiten determinar objetivamente qué modelo tiene el poder explicativo superior.
De la Simplicidad a la Probabilidad
Queremos elegir el modelo que explique los datos más simplemente.
¿Qué es la simplicidad? Es la ausencia de complejidad, la ausencia de partes o la ausencia de opciones. Otra forma de verlo es que hay muchas más maneras de hacer un modelo complejo que un modelo simple. Por lo tanto, una manera de medir la complejidad de un modelo es contar cuántas formas hay para construir un modelo como este. Entonces, suponiendo que no conocemos los detalles de cómo los procesos naturales generarían el patrón particular (o cómo lo elegiría un agente inteligente), suponemos que cada patrón en particular tiene la misma probabilidad de ser generado (o elegido). En otras palabras, la probabilidad de cualquier modelo en particular es el inverso de la cantidad de modelos similares. En general, los modelos simples son menos numerosos, y los modelos simples se consideran intuitivamente más probables. Por otro lado, los modelos complejos son mucho más numerosos y, por lo tanto, se consideran menos probables. Otra forma de verlo es que la complejidad es un costo que queremos evitar: los modelos simples son parsimoniosos.
Esta correspondencia entre complejidad e improbabilidad es muy útil, y podemos utilizar los dos conceptos de manera intercambiable para ayudar a organizar nuestro pensamiento. ¿Qué pasa si tiene un grupo de modelos complejos pero similares que explican los datos bastante bien? Luego los agrupa en un modelo más probable, que es un poco como un modelo grueso en un modelo más simple con menos elementos específicos.
En la selección de modelos Bayesianos, el mejor modelo es el que hace que los datos sean más probables. No tiene sentido tener un modelo simple si no explica los datos (si la probabilidad de los datos es cero). Del mismo modo, no tiene sentido tener un modelo que sea más complejo (y, por lo tanto, menos improbable) que los datos que necesita explicar. Eso sería excesivo. La complejidad general es la probabilidad de que el modelo se combine con la probabilidad de que los datos se den en el modelo. En el artículo de Ewert, hay dos modelos generales que queremos distinguir: el árbol de antepasado común y el gráfico de dependencia, pero hay una miríada de posibles submodelos, cada uno de los cuales contribuye a la probabilidad general del modelo superior.
Valores medios y suposiciones bayesianas
Infortunadamente, ambos modelos (el árbol de la vida y el gráfico de dependencia) son extremadamente complejos, con una gran cantidad de parámetros ajustables. Esto podría hacer que la pregunta aparente ser indeterminable: a menudo argumentamos que el árbol de la vida encaja de manera terrible con los datos, lo que requiere numerosos «epiciclos» ad-hoc para hacer que los datos encajen. Podríamos argumentar además que un gráfico de dependencia particular se ajusta mejor a los datos. Pero un creyente en antepasado común podría razonablemente responder que nuestra teoría tampoco es parsimoniosa; si agrega suficientes módulos podría explicar literalmente cualquier cosa, incluso datos aleatorios. Parece que decidir entre los dos modelos nunca puede ser una decisión racional; parece que siempre implicará una buena dosis de intuición o incluso de fe. Afortunadamente, sin embargo, hay formas de dominar la complejidad lo suficiente como para obtener respuestas objetivas y significativas.
La estrategia principal para hacer frente a la complejidad es la suma (o la integración matemática) sobre todas las posibilidades. Ewert maneja muchos de los parámetros por integración: estos incluyen la probabilidad de borde b (la conectividad esperada) de los nodos y las diferentes propensiones a agregar α o perder λ genes en cada uno de los n nodos. Esto puede parecer extraño, pero es un razonamiento probabilístico estándar. Si la distribución de probabilidad de Y (por ejemplo, el número real de pérdidas de genes) depende de X (por ejemplo, λ), pero no conoce X, puede calcular la probabilidad de Y si tiene la distribución de probabilidad de X. En muchos casos, ni siquiera sabemos cuál sería la verdadera distribución de X. En tales casos, Ewert supone que cada posibilidad tiene una probabilidad igual (una distribución plana) porque esto debería introducir el menor sesgo. Esto también puede parecer extraño, pero es bastante común en el razonamiento bayesiano, donde se lo llama una probabilidad a priori. Aunque la distribución previa de X es técnicamente una elección, y sí, esa elección tiene alguna influencia en el resultado, la forma en que funciona el razonamiento Bayesiano es que cuantos más datos añada, menos elección particular tendrá. Lo importante es elegir un dato a priori que no esté sesgado; una probabilidad a priori que permita que los datos hablen, si lo desea. El razonamiento bayesiano es importante porque nos da cierta esperanza de escapar de la tiranía de los supuestos fundamentalistas, ya sea fundamentalismo evolucionista / naturalista o fundamentalismo creacionista / bíblico (aunque curiosamente Thomas Bayes era clérigo).
La idea es que queremos asegurarnos de que las muchas cosas que no sabemos no nos impidan hacer inferencias razonables utilizando lo que sabemos.
Cálculo de límites
Aunque algunas de las variables se pueden integrar matemáticamente, otras no. Este es un problema para ambos modelos ya que (en teoría) deberíamos sumar todas las probabilidades de todas las posibles asignaciones de genes a nodos y eliminaciones de nodos. Pero es un problema particular para el gráfico de dependencia: hay diferentes números posibles de nodos en el gráfico de dependencia, y una miríada de formas posibles de conectar cada número de nodos. Para obtener una probabilidad precisa para el modelo general de gráficos de dependencia, necesitaríamos resumir cada una de estas posibles configuraciones. En la práctica, estas sumas son imposibles de hacer; hay demasiados.
Sin embargo, incluso cuando no es posible calcular una probabilidad precisa, a menudo es posible calcular límites. Esta es una forma consagrada de probar cosas sin hacer cálculos difíciles, especialmente en matemáticas.
¿Cuál es la probabilidad de que una tetera se una a partir de átomos en órbita alrededor del sol? Nadie lo sabe. Pero, por ejemplo, podría decirse que es al menos tan improbable como una colección de 100g de átomos que superan la entropía termodinámica para mantenerse unidos. Este es un límite superior de la probabilidad, y es algo que se puede calcular con bastante facilidad (y, como resulta, es extremadamente improbable, efectivamente imposible).
Para mostrar que el gráfico de dependencia es una mejor explicación, Ewert estima un límite superior en la probabilidad de los datos dada la hipótesis del árbol ancestral, y calcula un límite inferior en la probabilidad de los datos dada la hipótesis del gráfico de dependencia, y luego mira en la diferencia.

Complejidad del gráfico
El modelo de árbol tiene una gran ventaja ya que es más simple que el modelo de gráfico de dependencia. Si hay S especies, entonces el modelo de árbol tiene (S-1) especies ancestrales. En contraste, el gráfico de dependencia puede tener hasta Nmax = (2S-1-s) módulos opcionales. A medida que S se hace más grande, esta diferencia crece exponencialmente. Por ejemplo, cuando hay 4 especies (como en las figuras a continuación), hay hasta 3 especies ancestrales, pero hasta 11 módulos. Donde solo hay 10 especies, hay 9 especies ancestrales, ¡pero hasta 1013 posibles módulos! Eso es mucha complejidad adicional.
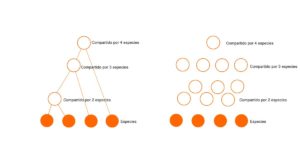
En segundo lugar, las conexiones agregan complejidad. Un árbol de N nodos tiene exactamente (N-1) conexiones, pero un gráfico de N nodos puede tener alrededor de N hasta N(N-1)/2 conexiones posibles. Cada una de estas conexiones pueden existir o no, dando un gran número de posibilidades. La probabilidad de cualquier combinación particular de conexiones es muy pequeña, lo que se traduce en una probabilidad muy pequeña para cualquier gráfico en particular.
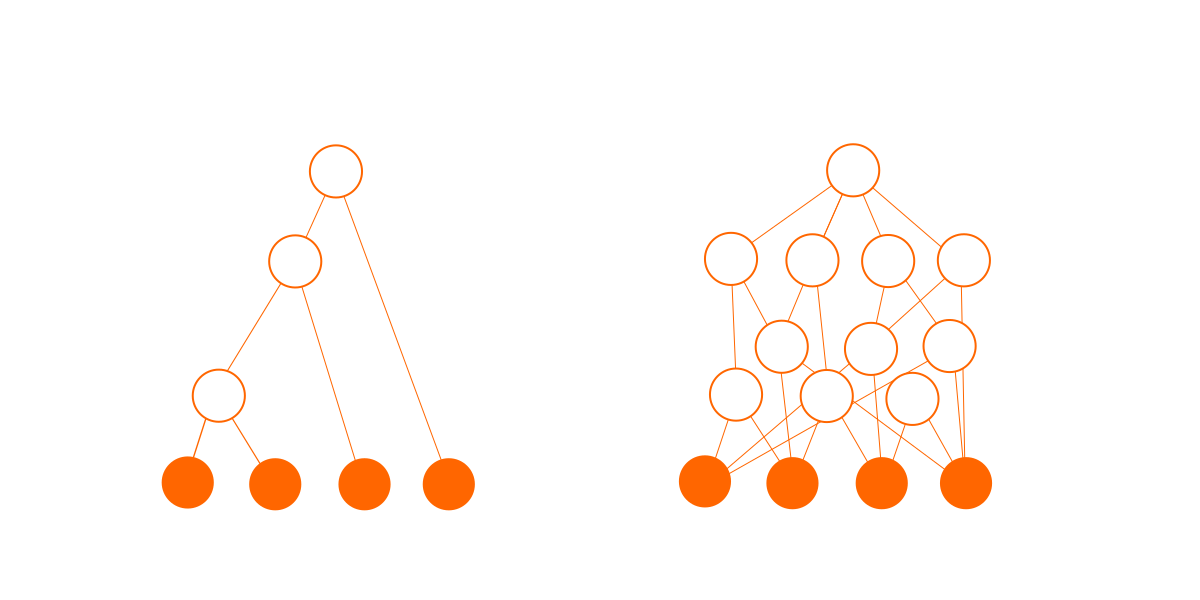
Este gráfico de dependencia no es real; es solo mi impresión artística para mostrar el aumento potencial de la complejidad.
Para el modelo de árbol, Ewert supone que los biólogos han hecho un buen trabajo bajo las limitaciones de su modelo y ya encontraron un ajuste de buena calidad, por lo que toma el hipotético árbol ancestral desarrollado por expertos biólogos encontrados en NCBI. Debido a que estamos calculando límites, no probabilidades precisas, y porque el árbol es mucho más simple, el cálculo se puede simplificar dando al árbol una probabilidad condicional de 1 (en palabras: si la hipótesis del árbol es verdadera, entonces este árbol es el modelo correcto). Por el contrario, cada gráfico de dependencia se trata como altamente improbable; hay una fuerte penalización solo por ser un gráfico de dependencia.
Si todo lo demás fuera igual, sería mucho más parsimonioso elegir el árbol sobre el gráfico de dependencia. Entonces, ¿por qué alguien optaría por el gráfico de dependencia? Es por los datos.
Complejidad de los datos dado el gráfico
Los dos modelos reciben la misma información para explicar. Los datos que Ewert eligió fue la distribución de las familias de genes en las especies. Estas familias de genes también fueron tomadas de categorías y datos creados por biólogos expertos, que se encuentran en nueve bases de datos públicas diferentes.
El algoritmo de Ewert luego asigna estas familias de genes a especies ancestrales en el árbol, o módulos en el gráfico de dependencia, para optimizar la probabilidad de cada una. Ewert sigue la suposición la Ley de Dollo, lo que significa que cada familia de genes aparece solo una vez en la historia de la vida, o en no más de un módulo diseñado.
El algoritmo asigna inicialmente cada familia de genes el supuesto de ancestro común (de acuerdo con la hipótesis del árbol) y luego trata de mejorarlo. El árbol y estas asignaciones de genes también se usan como una primera suposición para el gráfico de dependencia. Por defecto, los nodos obtienen todos los genes de los nodos superiores a los que están conectados. En el caso del árbol, esto significa que las especies descendientes heredan genes de especies ancestrales. En el caso del gráfico de dependencia, esto significa que los módulos importan genes de sus dependencias. Para que el gráfico se ajuste, algunos genes pueden necesitar ser eliminados una o más veces de los nodos inferiores.
Ewert supone que hay una cierta probabilidad de agregar un gen a cada nodo, pero dado que no sabemos cuál es, promedia todas las probabilidades posibles. La fórmula también se da en la ecuación 4 del artículo. También asume que las supresiones de genes ocurren con una cierta probabilidad en cada nodo, pero dado que no sabemos cuál es esa probabilidad, promedia todas las probabilidades posibles. La fórmula también se da en la ecuación 6 del documento. El efecto es que la primera adición/eliminación cuesta una penalización que depende del número de genes, y luego las adiciones/eliminaciones subsiguientes cuestan un poco menos, y así sucesivamente. La consecuencia es que puede ser más probable agregar un gen más arriba en el árbol/gráfico o eliminarlo más abajo en el gráfico, incluso si eso significa eliminarlo más veces. De modo que también hay un algoritmo que intenta mover las asignaciones de la familia de genes en el árbol o gráfico, y / o eliminaciones en el árbol o gráfico, si eso le da una mejor probabilidad. En el caso de los gráficos de dependencia, el algoritmo también crea o elimina módulos completos donde eso daría mejores probabilidades. Este último algoritmo es lo que permite el descubrimiento de gráficos de dependencia que son radicalmente diferentes de un árbol.
Considere estos dos conjuntos imaginarios de datos. Cada fila o color es una familia de genes, y cada columna es una especie. Un círculo lleno indica que esa especie tiene un representante de esa familia de genes en su genoma.

El primer conjunto de datos (a la izquierda arriba) se ajusta perfectamente a un árbol (abajo a la izquierda). El gráfico de dependencia óptimo (abajo a la derecha) parece idéntico al árbol, pero debido a las penalizaciones adicionales por ser un gráfico de dependencia, se pierde: la mejor explicación para estos datos es un árbol.
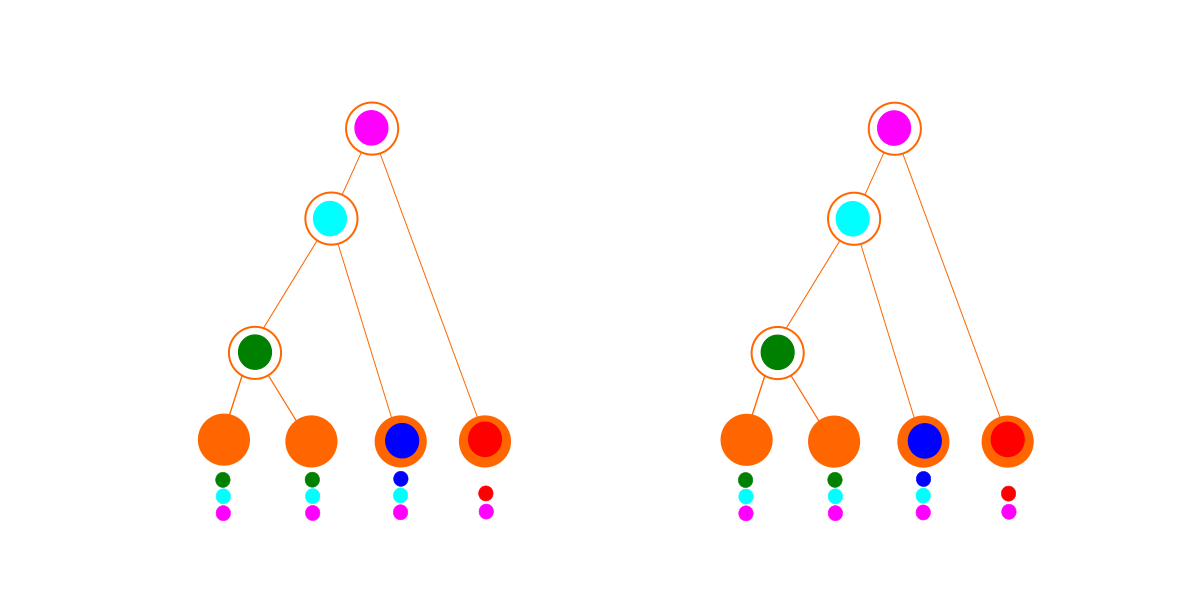
Para el segundo conjunto de datos, aún podemos caber en un árbol (abajo a la izquierda), pero es un desastre. Tenemos que eliminar genes tantas veces para que encaje la hipótesis sea bastante improbable. Por el contrario, el algoritmo de búsqueda de gráficos de dependencia encuentra un conjunto de módulos sin eliminaciones. Como resultado, el gráfico de dependencia (abajo a la derecha) gana para este conjunto de datos. En la práctica, con datos más complicados, el mejor gráfico de dependencia también puede implicar algunas eliminaciones. (El hecho de que un módulo sea importado no necesariamente significa que se usa todo en él, y también es posible que una especie diseñada haya perdido genes que alguna vez tuvo).
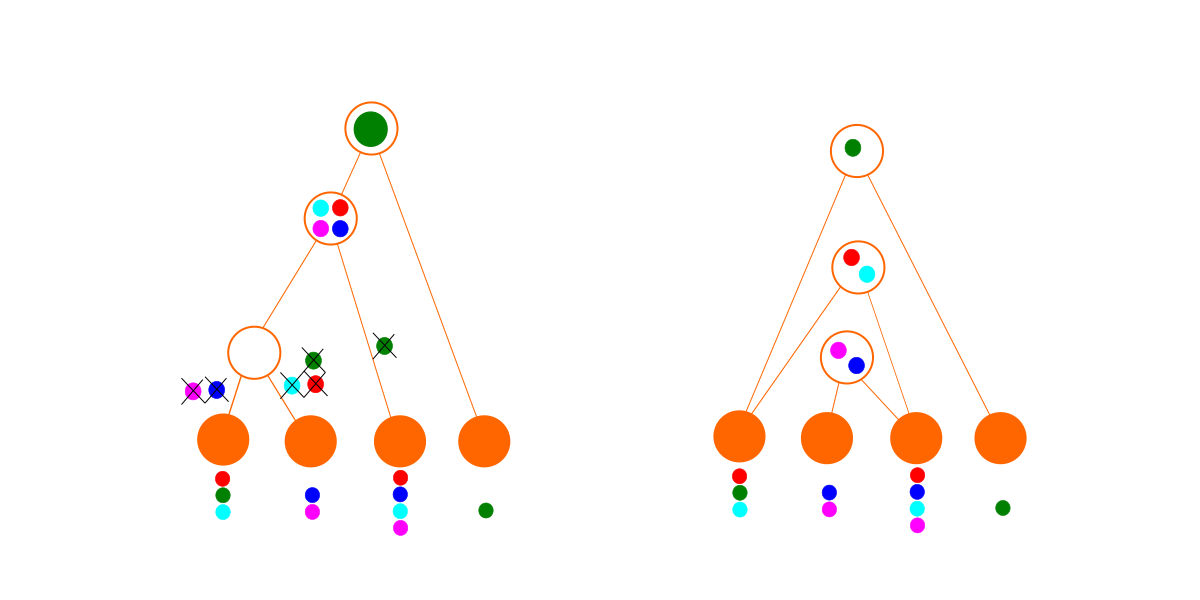
El método no tiene que encontrar el mejor gráfico de dependencia, porque sabemos que el mejor gráfico de dependencia es al menos tan bueno como el mejor que encontramos, y por lo tanto el gráfico de dependencia es al menos mucho mejor que la hipótesis del árbol.
Aplicando el Método
Así es como funciona el método de selección de modelos en principio. En el documento, se puede ver que Ewert probó el método al generar gráficos de software real, de varias simulaciones evolutivas y de datos aleatorios (una hipótesis nula en la que los genes de cada especie se extrajeron aleatoriamente de un único conjunto común). Encuentra que identifica correctamente los árboles de los procesos evolutivos (aunque la evolución es simulada) e identifica correctamente los gráficos de dependencia del software compilado, e identifica correctamente también los datos aleatorios.
Lo realmente emocionante es lo que sucede cuando mira los datos biológicos. Independientemente de cómo la biología sea distinta del software, el extraño resultado es que el panorama general de la biología parece ser objetivamente mucho más parecido al software que a la evolución.
Un último comentario
Finalmente, una de las razones por las que amo este artículo es porque ayuda a explicar por qué el árbol de la vida de Darwin ha sido aceptado por muchas personas razonables hasta ahora. La razón es que cuando no hay mucha información, el modelo más simple gana por defecto. Pero ahora que tenemos más datos biológicos que nunca, y ahora que nuestra propia comprensión del diseño / ingeniería / tecnología se ha incrementado en formas que Darwin nunca podría haber imaginado, podemos comenzar a ver que un modelo un poco más complejo podría ser una explicación mucho más poderosa.
Artículo publicado originalmente en inglés por Andrew Jones Ph.D.
Foto: Árbol de la vida, en Walt Disney World Resort, por KirkMoorePhoto [CC BY-SA 4.0], de Wikimedia Commons.